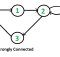
Graph Depth First Search

Depth First Search : Depth-first search (DFS) is an algorithm for traversing graph data structures. One starts at the root and explores as far as possible along each branch before backtracking.

DFS is typically used to traverse an entire graph, and takes time Θ(|V| + |E|).

Algorithms that use depth-first search as a building block include:

Finding connected components.
Topological sorting.
Finding 2-(edge or vertex)-connected components.
Finding 3-(edge or vertex)-connected components.
Finding the bridges of a graph.
Generating words in order to plot the Limit Set of a Group.
Finding strongly connected components.
Planarity testing[7][8]
Solving puzzles with only one solution, such as mazes. (DFS can be adapted to find all solutions to a maze by only including nodes on the current path in the visited set.)
Maze generation may use a randomized depth-first search.
Finding biconnectivity in graphs.

package com.test.graph.algo;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
/*
 * @author rrohit
 */
public class DFS {
	private static boolean [] visited;
	private static int count;
	
	/*
	 * Without recursion approach
	 */
	public static void dfs(Graph g){
		
		visited = new boolean[g.getVertices().size()];
		Stack<Graph.Vertex> stack = new Stack<Graph.Vertex>();
		
		if (g.getVertices().size() == 0){
			System.out.println("Graph Is Empty :: Return");
			return;
		}
		
		visited[0] = true;
		stack.add(g.getVertices().get(0));
		System.out.println("Vertex Visited: "+stack.peek()); // similar to stack.top()
		Graph.Vertex v,w;
		while(!stack.isEmpty()){
			count++;
			v = stack.peek();
			if ( (w = getAdjUnvisitedVertex(v, g)) != null){
				stack.add(w);
				visited[g.getVertices().indexOf(w)] = true;
				System.out.println("Vertex Visited: "+w);
			}else {
				stack.pop();
			}
		}
		System.out.println("Total Count = "+count);
	}
	
	public static Graph.Vertex getAdjUnvisitedVertex(Graph.Vertex v, Graph g){
		
		for (Graph.Edge e : v.getEdges()) {
			count++;
			if (e.getFrom().equals(v) && !visited[g.getVertices().indexOf(e.getTo())]){
				return e.getTo();
			}
		}
		return null;
	}
	
	public static void dfsRecurssive(Graph g, Graph.Vertex v){
		System.out.println("Visited : "+v);
		v.visited = true;
		
		for (Graph.Edge e : v.getEdges()) {
			Graph.Vertex w = e.getTo();
			if (!w.visited){
				dfsRecurssive(g,w);
			}
		}
	}
	
	public static void main(String[] args) {
		
		List<Graph.Vertex> vertices = new ArrayList<Graph.Vertex>(); 
		Graph.Vertex A = new Graph.Vertex('A');
		Graph.Vertex B = new Graph.Vertex('B');
		Graph.Vertex C = new Graph.Vertex('C');
		Graph.Vertex D = new Graph.Vertex('D');
		Graph.Vertex E = new Graph.Vertex('E');
		Graph.Vertex F = new Graph.Vertex('F');
		Graph.Vertex G = new Graph.Vertex('G');
		Graph.Vertex H = new Graph.Vertex('H');
		vertices.add(A);
		vertices.add(B);
		vertices.add(C);
		vertices.add(D);
		vertices.add(E);
		vertices.add(F);
		vertices.add(G);
		vertices.add(H);
		
		List<Graph.Edge> edges = new ArrayList<Graph.Edge>();
		edges.add(new Graph.Edge(0,A,B));
		edges.add(new Graph.Edge(0,B,C));
		edges.add(new Graph.Edge(0,B,H));
		edges.add(new Graph.Edge(0,C,D));
		edges.add(new Graph.Edge(0,C,E));
		edges.add(new Graph.Edge(0,E,H));
		edges.add(new Graph.Edge(0,E,F));
		edges.add(new Graph.Edge(0,E,G));
		
		Graph g = new Graph(vertices, edges);
		dfs(g);
		dfsRecurssive(g, A);
	}
}