Design an algorithm that calculates minimum degree of connection between given two users

package com.test.graph.algo;

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.List;
import java.util.Queue;
/*
 * Expedia----
 * I rephrase the original question as the following: Let say in Facebook, 
 * given two person A and B. Write a function to find out whether A is a friend or a friend 
 * of a friend of ... of B.
 */
import java.util.Stack;

/* Amazon--
 * Consider any social networking website like facebook etc. 
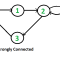
 * Design an algorithm / function that calculates minimum degree of connection 
 * between given two users. Assume that you are have already written function that 
 * returns a list of friends of given user :
 * getFriends(username/id) : its similar to getting no of edges for the given vertex.
 */


public class DegreeOfSeparation {

	DiGraph.Vertex [] pathTo;
	
	public DegreeOfSeparation(int size){
		pathTo = new DiGraph.Vertex[size];
	}
	
	/*
	 * Traverse till target vertex t is not visited,once t is visited hence we have found
	 * the shortest path between given friend A and B.
	 */
	public void bfs(DiGraph g, DiGraph.Vertex v, DiGraph.Vertex t){
		Queue<DiGraph.Vertex> queue = new ArrayDeque<>(g.getVertices().size());
		queue.add(v);
		v.setVisited(true);
		DiGraph.Vertex w;
		boolean found = false;
		while (!queue.isEmpty() && !found) {
			v = queue.remove();
			for (DiGraph.Edge e : v.getEdges()) {
				w = e.getTo();
				if (!w.isVisited()) {
					queue.add(w);
					w.setVisited(true);
					pathTo[g.getIndexOf(w)] = v;
				}
				if (t.isVisited()) {
					found = true; // traverse till t is not visited
					break;
				}
			}
		}
	}
	
	public void printPath(DiGraph g, DiGraph.Vertex s, DiGraph.Vertex t){
		//call bfs to prepare the path
		bfs(g, s, t);
		Stack<DiGraph.Vertex> stack = new Stack<DiGraph.Vertex>();
		for (DiGraph.Vertex x = t; x != s; x = pathTo[g.getIndexOf(x)]) {
			stack.add(x);
		}
		stack.add(s);
		
		System.out.println("Shortest Path Between Source and Target");
		while (!stack.isEmpty()) {
			System.out.println(stack.pop());
		}
		
		//or if we want to print in format A is friend of a Friend of B
		System.out.println("["+s+"] is friend");
		for (DiGraph.Vertex x = t; x != s; x = pathTo[g.getIndexOf(x)]) {
			System.out.println("of a friend");
		}
		System.out.println(" of ["+t+"] ");
	}
	
	public static void main(String[] args) {
		List<DiGraph.Vertex> vertices = new ArrayList<DiGraph.Vertex>(); 
		DiGraph.Vertex A = new DiGraph.Vertex("A");
		DiGraph.Vertex B = new DiGraph.Vertex("B");
		DiGraph.Vertex C = new DiGraph.Vertex("C");
		DiGraph.Vertex D = new DiGraph.Vertex("D");
		DiGraph.Vertex E = new DiGraph.Vertex("E");
		DiGraph.Vertex F = new DiGraph.Vertex("F");
		DiGraph.Vertex G = new DiGraph.Vertex("G");
		DiGraph.Vertex H = new DiGraph.Vertex("H");
		vertices.add(A);
		vertices.add(B);
		vertices.add(C);
		vertices.add(D);
		vertices.add(E);
		vertices.add(F);
		vertices.add(G);
		vertices.add(H);
		
		List<DiGraph.Edge> edges = new ArrayList<DiGraph.Edge>();
		edges.add(new DiGraph.Edge(0,A,B));
		edges.add(new DiGraph.Edge(0,B,C));
		edges.add(new DiGraph.Edge(0,H,B));
		edges.add(new DiGraph.Edge(0,C,D));
		edges.add(new DiGraph.Edge(0,C,E));
		edges.add(new DiGraph.Edge(0,E,H));
		edges.add(new DiGraph.Edge(0,E,F));
		edges.add(new DiGraph.Edge(0,E,G));
		
		DiGraph g = new DiGraph(DiGraph.TYPE.UNDIRECTED, vertices, edges);
		DegreeOfSeparation dgs = new DegreeOfSeparation(g.getVertices().size());
		dgs.printPath(g, A, G);
	}
}